■
概要
●
本コマンドは、y=関数(x)または媒介変数で表現される2次元曲線を作成します。
●
任意の数式を入力することで懸垂曲線や渦巻き曲線などの曲線を作成することができます。
●
曲線は3次スプラインで補間することができ、よりスムーズな曲線も可能です。
●
代表的な方程式や曲線がテンプレートとして準備されています。
■
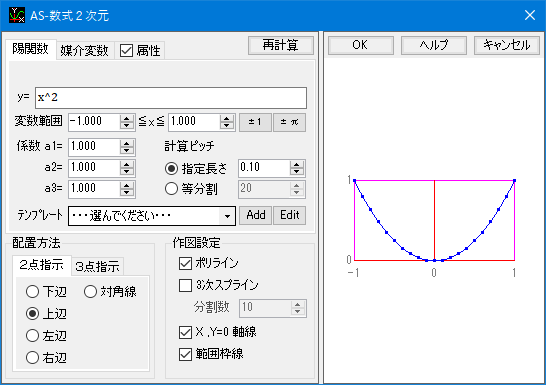
ダイアログ画面
■
陽関数
●
y=f(x) [x:変数]で表現される2次元曲線を作成します。
例えば、[y=-a1*x^2+1] [-1≦x≦1] [a1=1.0] とすると、以下のような放物線になります。
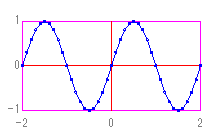
また、[y=sin(pai*x)] [-2≦x≦2] とすると、以下のようなサインカーブになります。
■
媒介変数
●
x=f(t),y=f(t) [t:媒介変数]で表現される2次元曲線を作成します。
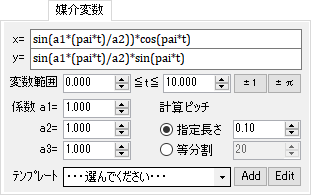
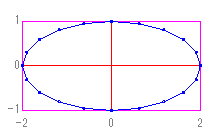
例えば、[x=a1*sin(pai*t)] [y=a2*sin(pai*t)] [-1≦t≦1] [a1=2.0] [a2=1.0] とすると、以下のような楕円になります。
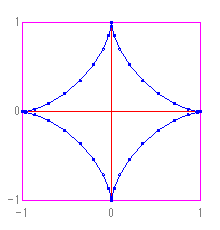
また、[x=cos(pai*t)^3] [y=sin(pai*t)^3] [-1≦t≦1] とすると、以下のようなアステロイド曲線になります。
■
計算できる有効な文字および数式
|
演算記号・常数
|
|
[ + ] または [ + ]
|
足し算
|
|
[ - ] または [ - ]
|
引き算
|
|
[ * ] または [ × ]
|
掛け算
|
|
[ / ] または [ ÷ ]
|
割り算
|
|
[ ^ ]
|
べき乗
|
|
[ | ]
|
寸勾配
|
|
[ ( ) ]
|
括弧
|
|
演算優先順位
|
[ ^ ]→[ * / | ]→[ + - ]
|
|
対応関数
(大文字、小文字区別なし)
|
|
sin()
|
サイン
|
|
cos()
|
コサイン
|
|
tan()
|
タンジェント
|
|
asin()
|
アークサイン
|
|
acos()
|
アークコサイン
|
|
atan()
|
アークタンジェント
|
|
sinh()
|
双曲線正弦(サイン)
|
|
cosh()
|
双曲線余弦(コサイン)
|
|
tanh()
|
双曲線正接(タンジェント)
|
|
sqr() または sqrt()
|
平方根
|
|
log()
|
常用対数
|
|
ln()
|
自然対数
|
|
exp()
|
指数関数
|
|
abs() または fabs()
|
絶対値
|
|
deg()
|
ラジアン → 度変換
|
|
rad()
|
度 → ラジアン変換
|
|
cint()
|
整数型変換(四捨五入)
|
|
int()
|
整数型変換(切り捨て)
|
|
補足
|
|
log(x)
|
常用対数 = ln(x) / ln(10)
|
|
asin(x)
|
アークサイン = atn(x / sqr(1 - x^2)) x
|
|
acos(x)
|
アークコサイン = PAI / 2 - asin(x) x
|
|
sinh(x)
|
双曲線正弦 = (exp(x) - exp( - x)) / 2
|
|
cosh(x)
|
双曲線余弦 = (exp(x) - exp( - x)) / 2
|
|
tanh(x)
|
双曲線正接 = (exp(x) - exp( - x)) / 2
|
|
ネイピア数
|
2.71828182845905・・・ = exp(1)
|
|
演算記号・常数
(大文字、小文字区別なし)
|
|
PAI,pai
|
パイ:3.141592653589793238462643383279
|
|
e+
|
例)1.5 e+5 →(=1.5×10^5)=150000
|
|
e-
|
例)1.5 e-5 →(=1.5×10^-5)=0.000015
|
会員専用プログラムのページへ